|
[VIEWED 30408
TIMES]
|
SAVE! for ease of future access.
|
|
|
|
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-01-06 1:15
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
can anyone solve: x^2 - 2^x =0 by algebraic method??? (x squared minus two to the power x equals zero) of course, without using graphing calculator.
|
| |
|
|
|
|
sujanks

Please log in to subscribe to sujanks's postings.
Posted on 03-01-06 8:32
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
ok, this is how i get x=2. x^2 = 2^x 2logx = xlog2 2/x. logx = log2 log(2/x)+ x = 2; log(2/x) = 2-x log x - log 2 = x-2; logx - x = log 2 - 2; so, x=2. couldn't solve for x=4;
|
| |
|
|
slash

Please log in to subscribe to slash's postings.
Posted on 03-01-06 8:56
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
I got A in Calculus I, tara yo dekhe pachi ta malai feri precalculus padhnu parne jasto lagyo hehehehe....
|
| |
|
|
jairamjiki

Please log in to subscribe to jairamjiki's postings.
Posted on 03-01-06 9:22
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
good job guys. keep it up. this kind of discussion is good for everyone.
|
| |
|
|
what more

Please log in to subscribe to what more's postings.
Posted on 03-02-06 12:37
AM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
. x^2 = 2^x 2 (ln x) = x (ln 2) (ln x)/x = (ln 2)/2 The following is the plot of the last expression, and you get two roots, 2 and 4. It is interesting to see what happens if it is not x-squared but higher orders. It seems like there are only two real roots for everything more than (raised to the power) 2 except e itself, in which case we have only one real root. But there has to be more roots for higher order, right? Like cubic expressions should have 3 roots. I guess the ones we don't see are imaginary roots? As q tends to infinity, (ln q)/q tends to 0. Also, this line (ln q)/q first increases then decreases. Of course, for q<1, we have only one root - see the plot.
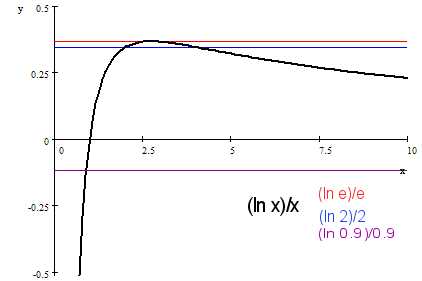
|
| |
|
|
what more

Please log in to subscribe to what more's postings.
Posted on 03-02-06 12:45
AM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
^ (ln q)/q increases then decreases with q for q>1
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-02-06 11:55
AM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
guys, thanx a lot for information, this equation doesn't just have the two positive roots..it does have a negative root also.like whatmore said, the higher degree eqns have more roots and the highest power of this equation is the variable itself. so the solution is x=2,4 and -0.767 plz see the graph attached......... havent taken the calc. 2 n 3 i believe log is the ultimate way for the solution...
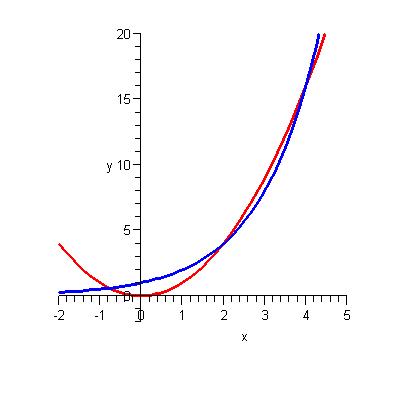
|
| |
|
|
stillReturns

Please log in to subscribe to stillReturns's postings.
Posted on 03-02-06 12:55
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
looking at all these i dont' think i ever went to skool at all... Or maybe i went to skool to look at chicks..lol
|
| |
|
|
sujanks

Please log in to subscribe to sujanks's postings.
Posted on 03-02-06 2:57
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
but still how do you solve it algebraicly
|
| |
|
|
divdude

Please log in to subscribe to divdude's postings.
Posted on 03-02-06 9:11
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
I couldnt find the exact solution, not even with the help of mathematica. That mathematica gave me one of the most complicated solution. Anyway I tried to slove it in analytical way for the general case, x^a=a^x ........(lets consider a is an integer and |a|>0) log(a)(x^a)=log(a)(a^x)..(this is not natural logarihtm it is the logarithm with base a) alog(a)(x)=xlog(a)(a) alog(a)(x)=x.........(cause log(a)(a)=1) a=x/log(a)(x).......................(1) From equation 1 we can conclude following things. 1.x is an integer. 2.value of x follows the following progression(a,a^a,a^(a^a) and so on) So it can be concluded from here that this equation can have two real roots only if a^(a^(a^.........)) upto nth term/a^(a^(a^..........)) upto n-1th term=a otherwise there is only one real root which is equal to a. Hehe hope someone can come with better solution.
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 12:24
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
div can u tell me what the mathmatica give u?
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 12:31
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
sujanks, how did you get this?????????? log(2/x)+ x = 2; log(2/x) = 2-x log x - log 2 = x-2;
|
| |
|
|
hyakula

Please log in to subscribe to hyakula's postings.
Posted on 03-03-06 12:39
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
How about this?? x^2-2^x=0 x^2=2^x log (x^2) = log (2^x) 2 log x = x log 2 log x / x = log 2 / 2 log x ^(1/x) = log 2 ^(1/2) This is true only if x = 2
|
| |
|
|
sujanks

Please log in to subscribe to sujanks's postings.
Posted on 03-03-06 1:31
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
i guess i went a step ahead log(2/x)+ x = 2; log(2/x) = 2-x ->log2 - logx = 2-x ->logx - log2 - x-2
|
| |
|
|
sujanks

Please log in to subscribe to sujanks's postings.
Posted on 03-03-06 1:32
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
read fourth line as: ->logx - log2 = x-2
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 1:50
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
i mean how does 2/x. logx = log2 imply log(2/x)+ x = 2
|
| |
|
|
sujanks

Please log in to subscribe to sujanks's postings.
Posted on 03-03-06 2:25
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
can't.. sorry my solution is wrong... but i am sure there is a way to find it algebraicly... trying every possibility
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 4:25
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
well i m trying it myself from few days............ i told one of my frens to ask her prof in MO.........she asked 3 teachers but they couldn't do....now i m sending it to my high school teacher in LA (not Los Angeles.)
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 4:26
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
sujanks bro thanks for your interest
|
| |
|
|
nevermind

Please log in to subscribe to nevermind's postings.
Posted on 03-03-06 4:41
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
Dunno how to prove it but try the following number all satisfy the criteria, short of time x^2 - 2^x = 0 x= - 0.767 x = 1 x= 2 x= 4 Its been ages I got into these stupid puzzles, and dont waste time thinking. Just answers dears, dont have time. Appreciate it I see all the graphs fail for x=1 bros so forget those stupid graphs
|
| |
|
|
tregor

Please log in to subscribe to tregor's postings.
Posted on 03-03-06 4:59
PM
Reply
[Subscribe]
|
Login in to Rate this Post:
0  ?
? 
|
| |
never mind bro when x=1, 1^2 -2^1 =1-2 =-1 therefore x=1 is not the solution the graph doesnt tell a lie
|
| |
